NUMERO DE SOLUCIONES DE UNA
ECUACION DE SEGUNDO GRADO
en la formula general de resolución
de ecuaciones de segundo grado observamos la expresión.
Una raíz cuadrada solo es posible
cuando el radicando es positivo.
A la expresión que esta dentro
del signo de raíz se le llama radicando.
El radicando se denomina
discriminante en el estudio de las soluciones de una ecuación de segundo grado.
Discriminante.
El número de raíces o soluciones
de una ecuación se puede determinar antes de resolver la ecuación con solo
estudiar el discriminante.
1: el discriminante es mayor que
cero (la ecuación tiene dos soluciones distintas).
2: el discriminante es cero (la ecuación
solo tiene una solución doble).
3: el discriminante es menor que
cero (la ecuación no tiene soluciones reales). Recordamos que no existen raíces
en las que el radicando sea negativo (menor a cero).
Ejemplo.
Estudiamos las soluciones de la
siguiente ecuación de segundo grado.
Formula general.
Discriminante.
El discriminante es menor que
cero, por lo tanto, la ecuación no tiene soluciones.
Ejemplo 2.
Estudiamos las soluciones de la
siguiente ecuación.
Formula general.
Discriminante.
El discriminante es cero, la ecuación
tiene una solución.













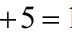


No hay comentarios.:
Publicar un comentario