RESOLUCION DE SISTEMAS DE ECUACIONES
LINEALES: METODO DE REDUCCION
Este método consiste en eliminar
una de las ecuaciones del sistema junto con una de las incógnitas, para así
obtener una ecuación de primer grado con una incógnita y despejar el valor numérico
de esa incógnita, posteriormente sustituimos ese valor en la ecuación más
sencilla del sistema para despejar la otra incógnita.
Podemos seguir estos pasos para
resolver un sistema de dos ecuaciones lineales.
1: multiplicamos una de las
ecuaciones por un número n (los dos miembros de la ecuación), tal que el
resultado iguale en valor absoluto a uno de los coeficientes de las incógnitas
y que sea de signo contrario al de la otra ecuación.
2: sumamos o restamos las dos
ecuaciones, de tal manera que se eliminara una de ellas junto con una
incógnita, quedándonos una ecuación de primer grado con una incógnita.
3: resolvemos esta ecuación obtenida
del proceso anterior para despejar la incógnita.
4: ya despejada la incógnita, la
sustituimos en una de las ecuaciones originales (lo podemos hacer en la más fácil).
5: resolvemos esta ecuación de
primer grado para despejar su incógnita.
Ahora ya tenemos los valores numéricos
de (x,y) que satisfacen el sistema.
Ejemplo
Resolvemos el siguiente sistema
de dos ecuaciones lineales.
Multiplicamos la primera ecuación
por 2 (para igualar el coeficiente de y, y que sea de signo contrario al de la
otra ecuación).
Sumamos las ecuaciones para
eliminar una de ellas y una incógnita (cuando es necesario también podemos
restar las ecuaciones).
El resultado es una ecuación de
primer grado con una incógnita, la resolvemos pare encontrar el valor numérico de
x.
Ya con el valor de x, lo
sustituimos en una de las ecuaciones del sistema, en este caso lo hacemos en la
primera, que es la mas sencilla.
Resolvemos esta ecuación para
obtener el valor numérico de y.
Ahora tenemos los valores de
(x,y) que satisfacen el sistema.
Comprobamos sustituyendo en el
sistema y verificando que la igualdad es cierta.



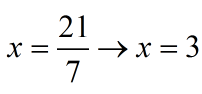







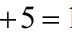


el procedimiento es fácil. Lo dificil es hacer que los alumnos se interesen a realizarlo sin la presión de obtener una nota. gracias
ResponderBorrarRobinson Ramírez A.